Verteilungen und Lageparameter
Überblick Link to heading
Die Realität wird in der heutigen Zeit ganz erheblich durch die Analyse und Bewertung von Daten vermittelt. Corona, Klimawandel, künstliche Intelligenz, Massenverfahren — viele komplexe Phänomene lassen sich ohne einen Blick in massive Datensätze kaum noch nachvollziehen oder sinnvoll bearbeiten. An diesem Punkt stoßen die rein literarischen Methoden der traditionellen Rechtswissenschaft an ihre Grenzen.
Für Menschen sind Daten in ihrem Rohformat ab einer bestimmten Größe nicht mehr verständlich.1 Diese Größe ist sehr schnell erreicht — meist schon bei wenigen Dutzend Datenpunkten. Deshalb fasst man Datensätze mit Methoden der Statistik zusammen, um sie auf ein menschlich verständliches und nutzbares Maß zu reduzieren.
Einzelne statistische Kennzahlen scheinen auf den ersten Blick eine bestechende und objektive mathematische Klarheit zu bieten. Der Mittelwert (auch: “Durchschnitt” oder “arithmetisches Mittel”) ist eine der beliebtesten Kennzahlen der Datenzusammenfassung. Er ist einfach zu verstehen, einfach anzuwenden und weit verbreitet. Bedauerlicherweise führt die unreflektierte Anwendung des Mittelwerts oft zu verzerrten Ergebnissen, der Verdeckung von Diversität und dem exklusiven Fokus auf unrealistische Ideale (z.B. der berühmte “Durchschnittsbürger”).
Wir besprechen in diesem Tutorial deshalb verschiedene Arten der Zusammenfassung von Daten, zunächst anhand von synthetischen Daten, dann anhand eines realen juristischen Datensatzes:
- Lageparameter (Mittelwert und Median)2
- Verteilungen (Histogramm, Dichtediagramm, Box-Plot)
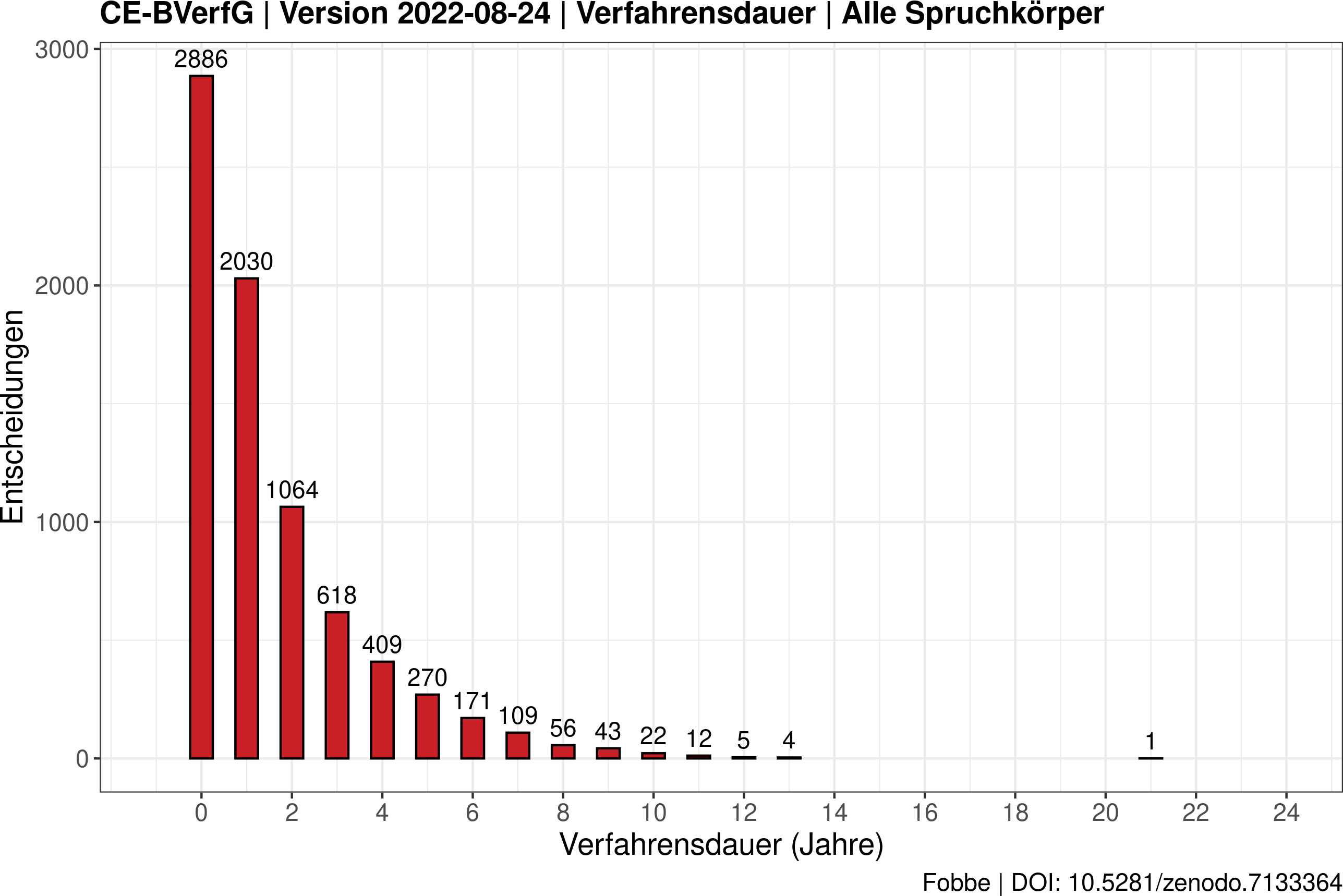
Verteilungen sind im Vergleich zu Lageparametern besser geeignet, Daten fair zusammenzufassen, weil der Informationsverlust geringer ist. Bei einer großen Anzahl von Datenpunkten gibt es oft nicht den einen charakteristischen Kennwert, sondern es gilt die unterschiedlichen Schwerpunkte und Tendenzen des Datensatzes aufzudecken. Ein Beispiel: so wäre es nach dem Blick auf folgendes Diagramm der Verfahrensdauern am BVerfG wohl fast schon irreführend, einen Durchschnitt von drei Jahren zu nennen (Fobbe 2022).
Variabilität und Unsicherheit Link to heading
Verteilungen können vor allem zwei Konzepte besser darstellen als Lageparameter: Variabilität und Unsicherheit.
Variabilität tritt in der Welt fast immer und überall auf. So mag der durchschnittliche Mann in Deutschland ca. 1,75 m groß sein, die tatsächliche Bandbreite und Verteilung menschlicher Körpergröße im Land ist aber kunterbunt. Viele Menschen werden um die 1,75 m sein, einige aber größer oder kleiner, einige wenige besonders viel größer und besonders viel kleiner. Auch ist der Unterschied zwischen den Geschlechtern für den Mittelwert — und damit die Position der Verteilung — ganz erheblich.
Unsicherheit liegt vor, wenn unser Wissen über einen Sachverhalt begrenzt ist, unabhängig von dessen Variabilität. So könnte beispielsweise ein Bankräuber exakt 1,90 m groß sein, die Zeugen ihn aber wegen der aufreibenden Situation und ungenauer Wahrnehmung nur als “zwischen 1,80 m oder 2,00 m” beschreiben können, bzw. einfach nur als “sehr groß”.
Variabilität ist eine Eigenschaft des Seins, Unsicherheit eine des Wissens. Beide können gleichzeitig auftreten. Die Berechnung und Visualisierung von Verteilungen erlaubt es uns, Variabilität und Unsicherheit quantitativ und rational zu begegnen.
Vorbereitung Link to heading
Wir benutzen die Programmiersprache R, um Daten zu generieren, zu analysieren und zu visualisieren. Der gesamte Code ist so gestaltet, dass Sie ihn zeilenweise in Ihre R-Konsole kopieren und selbst ausführen können.
Probieren Sie es aus! Lesen Sie das Tutorial nicht nur, sondern führen Sie auch den Code selbst aus! Um die Ergebnisse zu prüfen, die Details besser zu verstehen und selber ein wenig zu experimentieren. Die Freude am Programmieren kommt erst mit dem Selbermachen — nie mit dem Lesen allein.
Benutzen Sie für dieses Tutorial am besten WebR.
WebR ist eine Web-Anwendung, die direkt in ihrem Browser läuft und den R Code lokal auf ihrem eigenen Computer ausführt, nicht in der Cloud. Eine Installation ist nicht notwendig.
Selbstverständlich können Sie den Code aus dem Tutorial auch lokal mit einer typischen Entwicklungsumgebung wie RStudio oder in der Cloud mit Posit Cloud ausführen.
Zufallszahlen fixieren Link to heading
1set.seed(999)
Vertiefung: Zufallszahlengenerator
Die Funktion set.seed(999) fixiert die Initialisierung für den Zufallszahlengenerator. Wenn Sie die gleiche Initialisierung verwenden, sollten Sie auch die gleichen Zufallszahlen erhalten. Sie können problemlos darauf verzichten, dann sehen ihre Ergebnisse und Diagramme leicht anders aus als meine. Das wird im Ergebnis aber keinen Unterschied machen.
Daten generieren Link to heading
Wir erstellen mit den folgenden Code-Zeilen jeweils 1.000 zufällige Datenpukte aus drei verschiedenen klassischen stochastischen Verteilungen. Solche oder ähnliche Datenpunkte könnten aus einer empirischen Studie oder Umfrage stammen. Die Zahl 1.000 habe ich gewählt, weil viele repräsentative Umfragen mit einer Zahl von ca. 1.000 Befragten arbeiten und Sie dadurch ein bisschen Gefühl für die statistische Praxis entwickeln werden.
Wir üben mit diesen drei idealisierten Verteilungen zur Vereinfachung und Veranschaulichung der Methodik:
- Vereinfachung, weil wir dadurch das Herunterladen und Einlesen von Daten ausklammern können
- Veranschaulichung, weil jede der drei Verteilungen sehr charakteristische Eigenschaften hat, die bei der Erklärung typischer Probleme hilft
Wir analysieren diese Daten im Laufe des Tutorials, nur etwas Geduld!
Normalverteilung Link to heading
1normal <- rnorm(1000, mean = 100, sd = 15)
Log-Normalverteilung Link to heading
1lognormal <- rlnorm(1000, meanlog = 4.47, sdlog = 0.5)
Beta-Verteilung Link to heading
1beta <- rbeta(1000, 0.2, 0.2) * 190
Werte der Verteilungen anzeigen Link to heading
Zunächst probieren wir einmal die Rohdaten der Verteilungen direkt anzuzeigen. Das ist bei vielen kleinen Datensätzen — aber auch manchmal bei größeren Datensätzen — gar nicht so verkehrt, weil man direkt Muster erkennen und daraus Hypothesen oder Ideen für die Exploration der Daten generieren kann. Wenn gravierende Fehler in den Daten vorhanden sind, sieht man sie ebenfalls oft schon in diesem Stadium.
Mit dem Klammerzusatz [1:50] werden nur die ersten 50 Datenpunkte angezeigt. Die Einschränkung wähle ich hier, damit Sie in diesem Tutorial nicht durch endlose Zahlenwüsten scrollen müssen, um zum nächsten Abschnitt zu gelangen. Bei sehr großen Datensätzen wird außerdem die Konsole geflutet und das Interface friert ein oder stürzt ab. Das ist bei 1.000 Datenpunkten aber unwahrscheinlich, außer sie haben einen sehr, sehr alten Computer.
Normalverteilung anzeigen Link to heading
1print(normal[1:50])
1## [1] 95.77390 80.31161 111.92776 104.05106 95.84040 91.50964 71.82013
2## [8] 80.99813 85.48375 83.18486 119.88196 102.00966 114.08124 102.58807
3## [15] 114.36476 79.55971 101.02503 101.50986 113.52017 68.88464 81.57155
4## [22] 109.64566 94.60356 104.41053 83.12097 109.63398 83.39894 86.72739
5## [29] 76.68857 98.09982 135.73996 109.01914 102.69042 116.20797 96.29782
6## [36] 68.29395 94.44209 107.84302 107.76708 78.96234 92.71545 100.12747
7## [43] 80.76830 83.32632 104.50998 104.14718 69.23684 100.21285 108.73400
8## [50] 99.47910
Probieren Sie die Daten ohne die Einschränkung anzuzeigen! Statt print(normal[1:50]) benutzen Sie einfach print(normal) oder setzen andere Grenzen als 1:50!
Erst wenn man seine Konsole ein paar mal aus Versehen geflutet hat, erkennt man wie aussichtslos die manuelle Inspektion von manchen Datensätzen ist. Bei 1.000 Datenpunkten wird ihr System aber zumindest nicht abstürzen.
Log-Normalverteilung anzeigen Link to heading
1print(lognormal[1:50])
1## [1] 85.12648 257.71340 48.41812 140.10341 136.86963 34.38457 151.97229
2## [8] 169.33980 84.81856 50.08362 138.04280 169.14846 186.62926 127.13527
3## [15] 44.42033 51.78645 107.27701 221.26954 66.90303 42.03478 96.06316
4## [22] 107.17145 51.65440 41.74021 65.47462 211.78821 41.83182 97.50702
5## [29] 60.25510 107.93089 67.23228 202.07011 160.05965 74.40073 111.34302
6## [36] 131.56600 70.06619 72.66396 115.78188 82.68581 75.36887 118.73016
7## [43] 65.71656 99.97671 60.43055 176.53575 61.78021 72.46802 98.20388
8## [50] 49.97018
Beta-Verteilung anzeigen Link to heading
1print(beta[1:50])
1## [1] 1.820029e+02 1.180641e+01 1.899884e+02 1.363032e+02 1.367371e+01
2## [6] 1.092780e+02 2.324482e+01 1.790829e+02 4.682861e+01 1.899997e+02
3## [11] 1.029877e+02 2.068828e+00 1.758332e+02 1.136942e+01 1.895999e+02
4## [16] 1.461639e+01 1.801766e-02 4.144685e-05 1.899997e+02 1.847211e+02
5## [21] 4.433401e+01 1.027253e+02 7.646949e+01 1.664601e+02 1.843718e+01
6## [26] 1.885473e+02 1.644399e+02 2.383747e-01 2.190459e-05 2.669806e+01
7## [31] 1.788748e+02 7.946888e+00 1.198917e+01 1.900000e+02 1.840867e+02
8## [36] 1.718406e+02 1.323951e+02 9.033565e+01 1.833539e+02 1.900000e+02
9## [41] 1.899991e+02 1.898603e+02 8.795029e+01 1.154381e+01 7.248238e-02
10## [46] 1.022053e+01 6.038260e+01 9.061349e-03 1.872870e+01 1.076143e+02
Ergebnis Link to heading
Zahlensalat. Keine Erkenntnisse, oder? In den Daten sind schon Muster, wir haben nur keine Chance sie in dieser durcheinander gewürfelten Rohform zu erkennen.3
Histogramme Link to heading
Die erste Aufgabe bei jedem neuen Datensatz: visualisieren. Histogramme sind bei numerischen Daten eine der wichtigsten visuellen Methoden.
Histogramme teilen die gesamte Bandbreite einer numerischen Variable in gleichmäßige Klassen (hier sichtbar als Balken) auf und zeigen an, wie häufig Datenpunkte in diesen Klassen vorkommen. Klassen könnte man auch als “Bereiche” oder “Unterteilungen” umschreiben.
Histogramme sind eine gute Möglichkeit, um eine erste grobe Abschätzung der Verteilung einer Variable vorzunehmen.
Histogramm: Normalverteilung Link to heading
1hist(normal, breaks = 20)
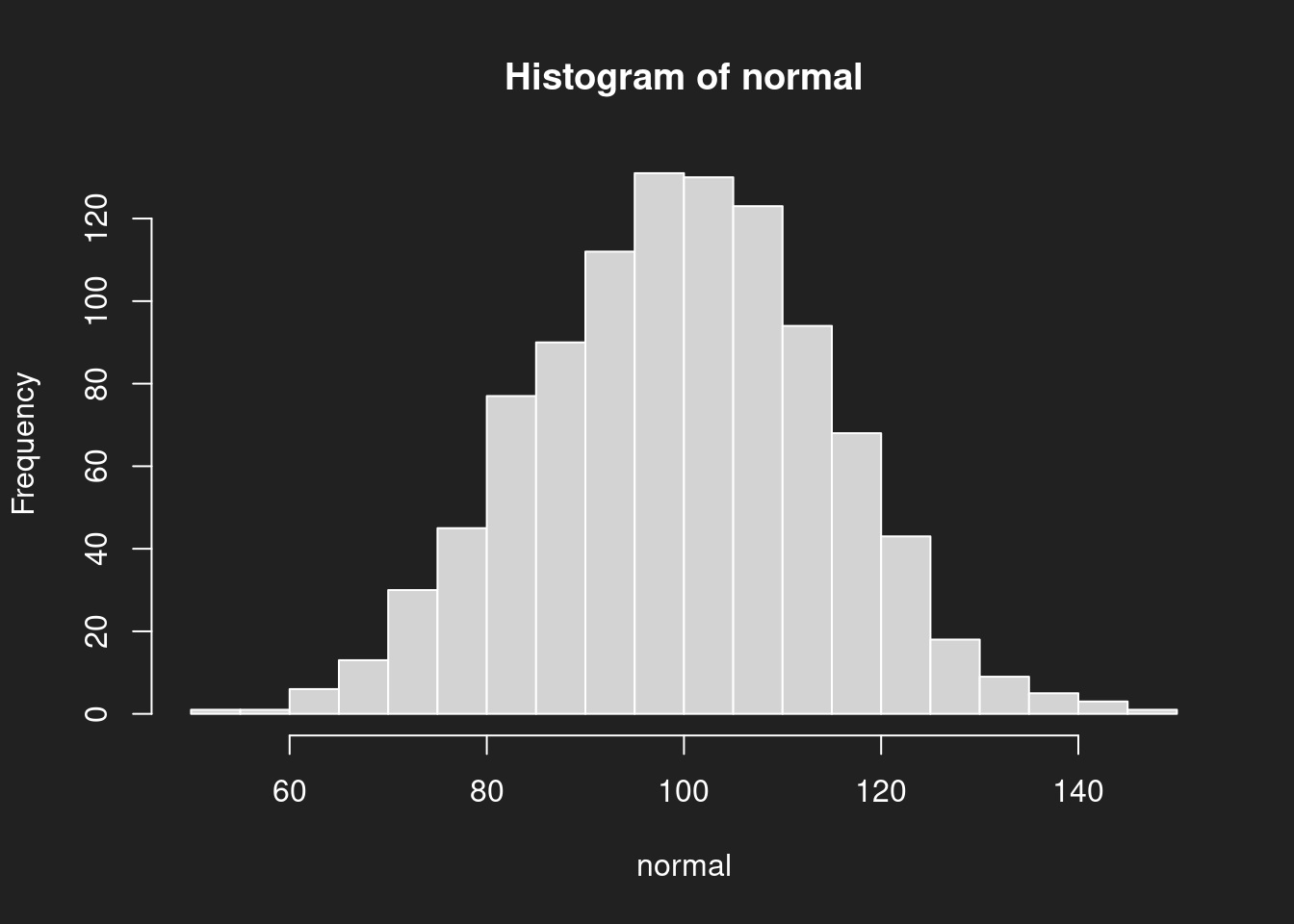
breaks = 20 bestimmt, wieviele Klassen genutzt werden. Probieren Sie andere Werte als 20 aus und beobachten Sie, wie sich das Histogramm ändert!Wir sehen hier schon die Andeutung der typischen Eigenschaften einer Normalverteilung:
- Symmetrie um den Mittelwert
- Besonders viele Datenpunkte in der Mitte
- Immer weniger Datenpunkte, je weiter wir uns vom Mittelwert entfernen.
Eine Normalverteilung hat nur einen Schwerpunkt, sie wird daher als unimodal bezeichnet.
Die Normalverteilung ist wegen ihrer glockenhaften Form auch als “Glockenkurve” bekannt, bzw. als “Gauß-Kurve” (nach Carl Friedrich Gauß). Man findet sie oft (aber nicht immer!) in der Natur. Beispielsweise ist die eingangs erwähnte menschliche Körpergröße in etwa normalverteilt.
Auch der Intelligenzquotient (IQ) wird als Normalverteilung mit Mittelwert 100 und Standardabweichung 15 modelliert, hier allerdings durch Konvention und kontinuierliche Standardisierung.4 Wenn Sie genauer in die von mir oben verwendeten Parameter blicken, werden Sie erkennen, dass ich hier genau diese Normalverteilung mit Mittelwert 100 und Standardabweichung 15 als Datenquelle gewählt habe.
Vertiefung: Standardabweichung
Die Standardabweichung ist der durchschnittliche Abstand aller Datenpunkte zum Mittelwert. Mit anderen Worten: jeder Wert hat seinen eigenen Abstand zum Mittelwert. Die Standardabweichung ist der Durchschnitt dieser Abstände. Wir werden das Thema an dieser Stelle nicht vertiefen, aber die Standardabweichung ist eine sehr wichtige Kennzahl in der Statistik und leidet an ähnlichen Problemen wie der einfache Mittelwert.
Histogramm: Log-Normalverteilung Link to heading
1hist(lognormal, breaks = 20)
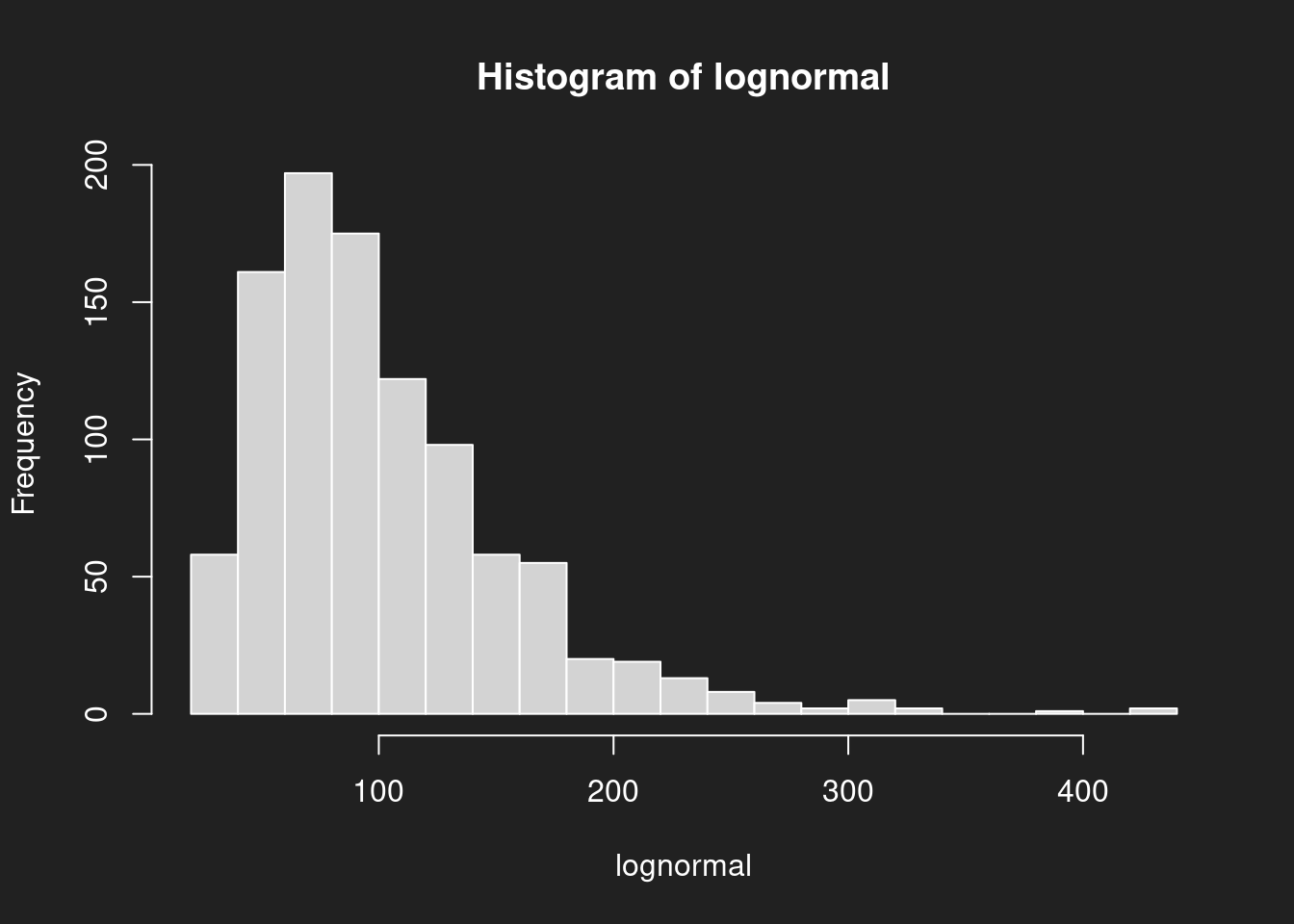
Die logarithmische Normalverteilung (oder “Log-Normalverteilung”) mit bestimmten Parametern sieht schon deutlich anders aus als die Normalverteilung. Vor allem: sie ist schief. Wenn der Schwerpunkt auf der linken Seite liegt, nennen wir sie “rechtsschief”. Klingt komisch, ist aber so.
Ähnlich aussehende Verteilungen (aber nicht zwingend dieselbe!) findet man bei juristischen Notenskalen, bei denen der Großteil der Studierenden Noten im Bereich der 4–6 Punkte erreicht, höhere Notenwerte aber immer seltener vergeben werden, je höher die Note ist. Anders als beispielsweise von iur.reform angenommen hat die juristische Notenverteilung nicht einmal annäherend die Form einer Normalverteilung (“Gauß-Kurve”), weil sie nicht symmetrisch ist und ihr Schwerpunkt deutlich nach links verschoben ist (Towfigh/Traxler/Glöckner 2014: 15–17).
Histogramm: Beta-Verteilung Link to heading
1hist(beta, breaks = 20)
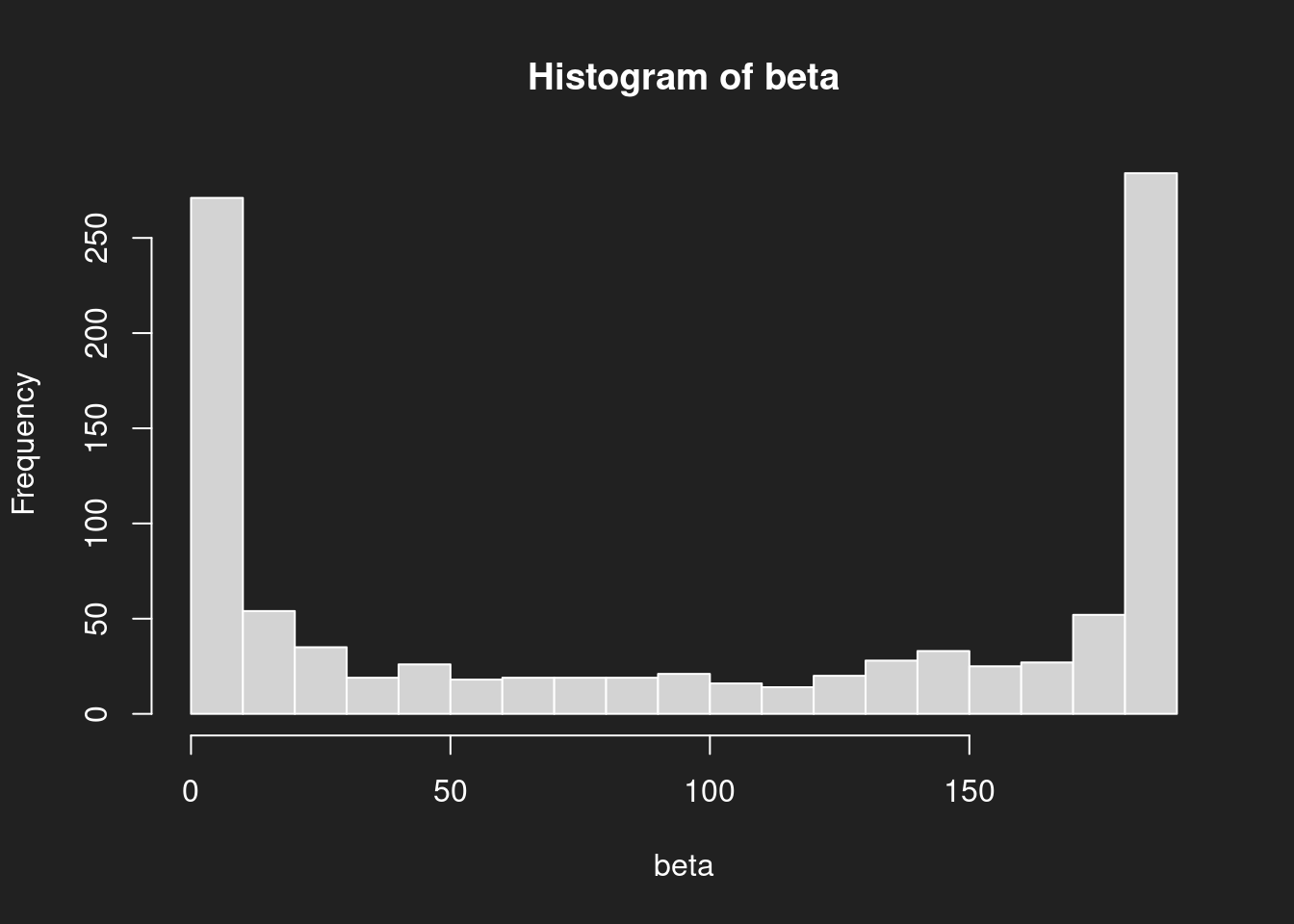
Die Beta-Verteilung in unserem Beispiel sieht nun wieder deutlich anders aus als die Normalverteilung oder die Log-Normalverteilung. Vor allem: sie hat zwei Schwerpunkte, will sagen sie ist bimodal.
Beta-Verteilungen können sehr verrückte Formen annehmen, sehen Sie sich auf Wikipedia einmal die verschiedenen Parametrisierungen an.
Zusammenfassung Histogramme Link to heading
Drei verschiedene Verteilungen, drei völlig unterschiedliche Formen und Schwerpunkte.
Mit dem Mittelwert hätten wir bei der Normalverteilung noch eine gute Beschreibung für den Schwerpunkt gehabt, bei der Log-Normalverteilung wären wir schon etwas daneben gelegen und bei der Beta-Verteilung komplett falsch.
Viele Missverständnisse des Mittelwerts beruhen darauf, dass Menschen sich implizit eine Normalverteilung um den Mittelwert herum vorstellen und den Mittelwert daher als repräsentativ ansehen (“Durchschnittsbürger”). Selbst bei einer echten Normalverteilung führt die Verwendung des Mittelwerts in der Praxis zu Problemen für nicht-durchschnittliche Menschen (man denke nur an besonders große Menschen und die immer enger werdenden Sitze in Flugzeugen).
Die Annahme einer Normalverteilung kann aber auch oft genug gravierend falsch sein und zu besonders falschen Vorstellungen bei der Interpretation des Mittelwertes führen. Sie sollten diese Annahme daher immer hinterfragen.
Vertiefung: Familien von Verteilungen
Nicht alle Normalverteilungen, Log-Normalverteilungen und Beta-Verteilungen sehen so aus, wie sie hier präsentiert wurden. Es handelt sich nämlich um Familien von Verteilungen, die durch ihre Parameter näher bestimmt werden. So könnte eine anders parametrisierte Log-Normalverteilung auch linksschief sein.
Dichtediagramme Link to heading
Dichtediagramme sind eine Verfeinerung von Histogrammen. Sie sind, grob gesprochen, eine Art von flüssiges Histogramm, bei denen die Klassen fließend ineinander übergehen. Ich bevorzuge Sie in meiner Arbeit meist gegenüber Histogrammen, weil ich mir dann keine Gedanken über die Anzahl der Klassen machen muss und die Ergebnisse schneller zu interpretieren sind.
Dichtediagramm: Normalverteilung Link to heading
1plot(density(normal))
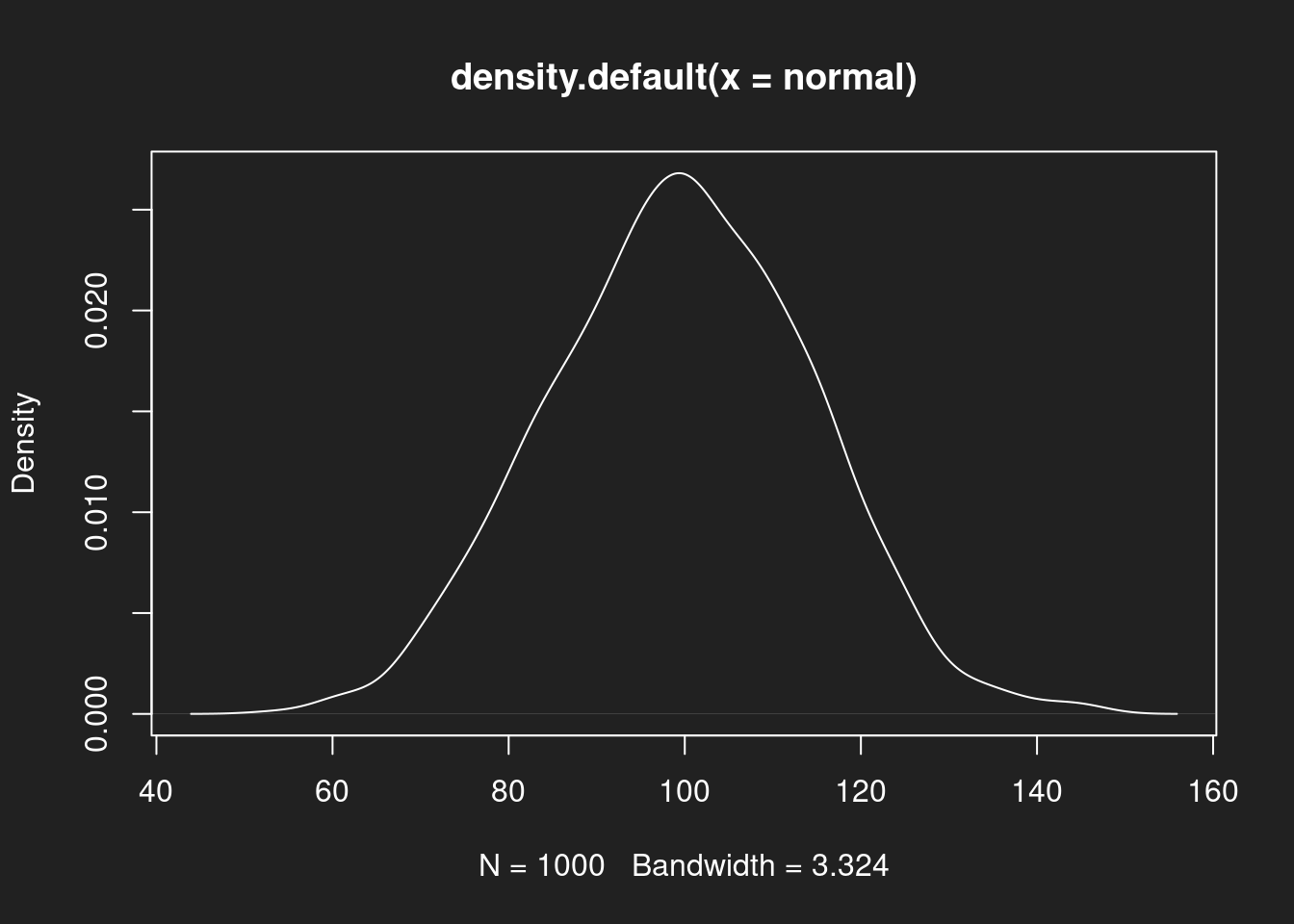
Dichtediagramm: Log-Normalverteilung Link to heading
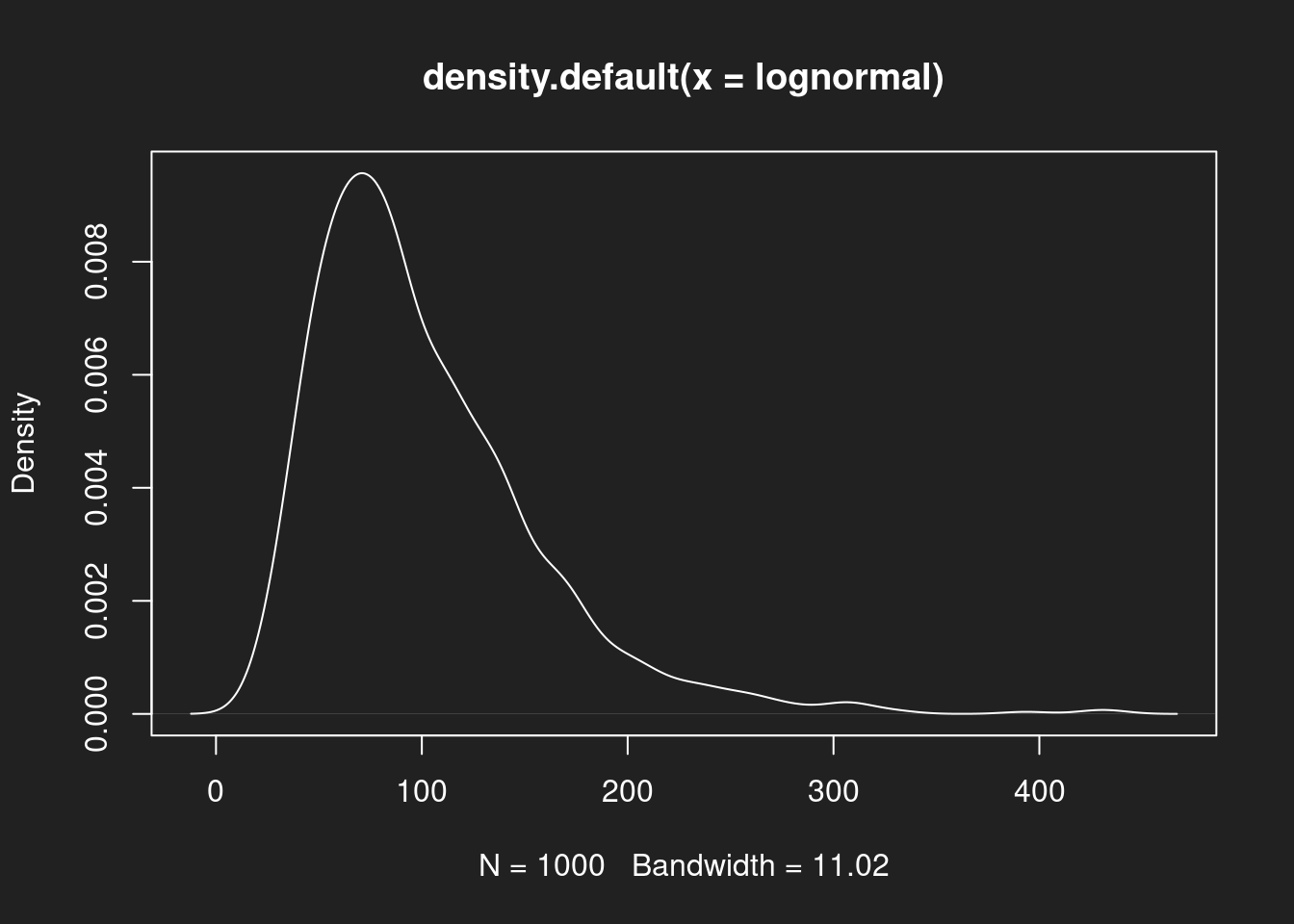
1plot(density(lognormal))
Dichtediagramm: Beta-Verteilung Link to heading
1plot(density(beta))

Zusammenfassung Dichtediagramme Link to heading
Wie bei den Histogrammen sehen wir zunächst eine symmetrische Verteilung mit einem Schwerpunkt bei der Normalverteilung, dann eine asymmetrische rechtsschiefe Log-Normalverteilung und schließlich eine symmetrische, aber bimodale Beta-Verteilung.
Lageparameter Link to heading
Um die wichtigsten sechs Kennwerte eines Datensatzes schnell zu bestimmen, können wir die bequeme Funktion summary() nutzen. Folgende Ergebnisse erwarten Sie:
| Kennwert | Beschreibung |
|---|---|
| Minimum | Der niedrigste Wert im Datensatz. |
| 1. Quartil | 1/4 der Datenpunkte sind kleiner als dieser Wert, 3/4 größer. |
| Median | Die Hälfte der Datenpunkte sind kleiner als der Median, die Hälfte sind größer. |
| Mittelwert | Die Summe aller Datenpunkte, geteilt durch die Anzahl der Datenpunkte. |
| 3. Quartil | 3/4 der Datenpunkte sind kleiner als dieser Wert, 1/4 größer. |
| Maximum | Der höchste Wert im Datensatz. |
Vertiefung: Five-Number Summary
summary() zeigt sechs Kennwerte an. Oft benutzt man für die Kennwerte einer Variable auch eine “Five Number Summary”, die in R mit fivenum() aufgerufen werden kann. Wir benutzen summary() um den Verglech mit dem Mittelwert anzuzeigen. Die Berechnungsmethode des Medians in fivenum() ist zudem leicht anders.
Lageparameter: Normalverteilung Link to heading
1summary(normal)
1## Min. 1st Qu. Median Mean 3rd Qu. Max.
2## 53.90 89.42 99.86 99.51 109.55 145.92
Bei der Normalverteilung sind Median und Mittelwert praktisch identisch. Beide bieten eine solide Beschreibung der zentralen Tendenz des Datensatzes. Dieses Idealbild haben viele Menschen im Kopf, wenn sie Mittelwert und Median interpretieren.
Lageparameter: Log-Normalverteilung Link to heading
1summary(lognormal)
1## Min. 1st Qu. Median Mean 3rd Qu. Max.
2## 20.93 63.22 88.01 101.34 128.54 433.77
Bei der Log-Normalverteilung liegen Mittelwert und Median deutlich auseinander. Wir sehen im Vergleich mit dem Histogram und Dichtediagramm, dass der Median eine deutlich bessere Beschreibung des Schwerpunktes darstellt. Der Mittelwert wird hingegen durch Ausreißer nach oben verzerrt.
Lageparameter: Beta-Verteilung Link to heading
1summary(beta)
1## Min. 1st Qu. Median Mean 3rd Qu. Max.
2## 0.000 6.764 98.912 96.506 184.584 190.000
Bei der hier gewählten Beta-Verteilung sind Mittelwert und Median insgesamt keine besonders guten Kennwerte, um die Daten zu beschreiben. Die bimodale Verteilung mit zwei Schwerpunkten an den Rändern kann durch einen einzelnen Kennwert nicht sauber beschrieben werden.
Zusammenfassung Lageparameter Link to heading
Wir haben für die gleichen Verteilungen Visualisierungen erstellt und Lageparameter berechnet. Bei dem Vergleich von Visualisierungen und Lageparametern wird klar, wie abhängig von der Form der Verteilung die Qualität der Lageparameter ist.
Box-Plots Link to heading
Box-Plots (auch “box-and-whiskers plots”) sind kompakte Visualisierungen einiger der eben beschriebenen Lageparameter aus summary(). Da sie aber nicht ganz intuitiv sind, hier eine kurze Erklärung der verschiedenen Bestandteile:
| Kennwert | Darstellung im Box-Plot |
|---|---|
| 1. Quartil | Linker Rand der Box |
| Median | Dicker Strich in der Mitte der Box |
| 3. Quartil | Rechter Rand der Box |
| $ 1,5 \times IQR $ | Die “Whiskers” |
| Ausreißer | Einzelne Punkte jenseits der Whiskers |
Box-Plot: Normalverteilung Link to heading
1boxplot(normal, horizontal = TRUE, boxwex = 0.3)

Für die Normalverteilung liefert der Box-Plot ein gutes Ergebnis. Die symmetrische Form und der Median als gute Beschreibung des Schwerpunkt ermöglichen dem Box-Plot eine gute Darstellung in diesem Fall.
boxwex = 0.3 bestimmt nur die Größe der Boxen in der Anzeige. Er hat keine mathematische Bedeutung.Box-Plot: Log-Normalverteilung Link to heading
1boxplot(lognormal, horizontal = TRUE, boxwex = 0.3)

Auch bei der Log-Normalverteilung bietet der Box-Plot eine vernünftige Visualisierung. Das liegt vor allem daran, dass der Mittelpunkt des Box-Plots auf dem Median beruht, nicht auf dem Mittelwert.
Box-Plot: Beta-Verteilung Link to heading
1boxplot(beta, horizontal = TRUE, boxwex = 0.3)
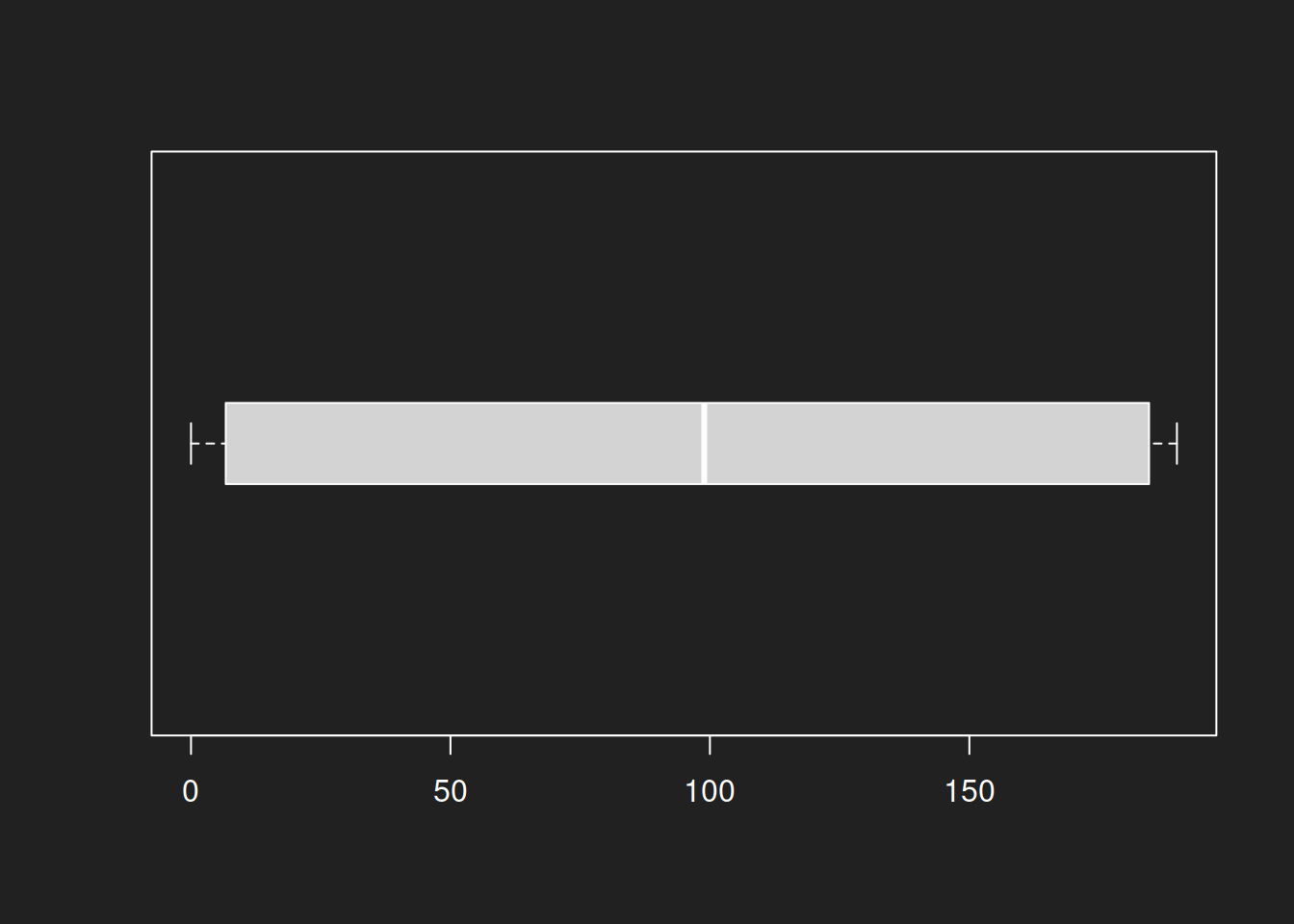
Bei dieser konkreten Beta-Verteilung ist ein Box-Plot wenig nützlich, ebenso wie die einzelnen Kennwerte von summary() selbst. Die bimodale Verteilung kann eine auf zentrale Tendenz und einzelne Kennwerte fokussierte Darstellung nicht sinnvoll abbilden.
Zusammenfassung Box-Plots Link to heading
Für Normalverteilung und Log-Normalverteilung liefern Box-Plots gute Ergebnisse. Das Diagramm für die Beta-Verteilung ist hingegen weitgehend nutzlos. Keine Überraschung, aber eine wichtige Lektion: immer unterschiedliche Visualisierungen probieren!
Übung: US Judge Ratings Link to heading
Vorbemerkung zum Datensatz Link to heading
Der Datensatz USJudgeRatings ist in R vorinstalliert und enthält von Anwält:innen vergebene Bewertungen zu 43 US-Amerikanischen Richter:innen eines US Superior Courts (Hartigan 1977).
Mit ?USJudgeRatings können Sie mehr über den Datensatz erfahren.
Die genaue Herkunft der Daten ist nicht zu rekonstruieren, die Ergebnisse sollten also nicht zu ernst genommen werden. Für Übungszwecke ist er jedoch hilfreich und gibt Ihnen einen Vorgeschmack auf “echte” Daten.
Erläuterung der Variablen Link to heading
Zur Orientierung, die Kurzbeschreibung der Variablen:
- CONT: Number of contacts of lawyer with judge
- INTG: Judicial integrity
- DMNR: Demeanor
- DILG: Diligence
- CFMG: Case flow managing
- DECI: Prompt decisions
- PREP: Preparation for trial
- FAMI: Familiarity with law
- ORAL: Sound oral rulings
- WRIT: Sound written rulings
- PHYS: Physical ability
- RTEN: Worthy of retention
Übungsaufgaben Link to heading
- Lassen Sie sich den gesamten Datensatz mit
print(USJudgeRatings)anzeigen! - Lassen Sie sich alle Variablen mit
names(USJudgeRatings)anzeigen! - Wenden Sie
summary()auf einzelne Variablen des Datensatzes an! Beispiel:summary(USJudgeRatings$CONT). - Visualisieren Sie einzelne Variablen mit
hist(),plot(density())undboxplot()! - Sie können
summary()undboxplot()auch auf ganze Datensätze anwenden, um diese extrem schnell zusammenzufassen. Probieren Sie einmalboxplot(USJudgeRatings, horizontal = TRUE, las = 1)aus!
Informationen zur strengen Replikation Link to heading
1sessionInfo()
1## R version 4.0.4 (2021-02-15)
2## Platform: x86_64-pc-linux-gnu (64-bit)
3## Running under: Debian GNU/Linux 11 (bullseye)
4##
5## Matrix products: default
6## BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
7## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.13.so
8##
9## locale:
10## [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
11## [3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
12## [5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
13## [7] LC_PAPER=en_US.UTF-8 LC_NAME=C
14## [9] LC_ADDRESS=C LC_TELEPHONE=C
15## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
16##
17## attached base packages:
18## [1] stats graphics grDevices utils datasets methods base
19##
20## other attached packages:
21## [1] knitr_1.39
22##
23## loaded via a namespace (and not attached):
24## [1] bookdown_0.27 digest_0.6.29 R6_2.5.1 lifecycle_1.0.3
25## [5] jsonlite_1.8.0 magrittr_2.0.3 evaluate_0.15 highr_0.9
26## [9] blogdown_1.10 stringi_1.7.8 cachem_1.0.6 rlang_1.1.1
27## [13] cli_3.6.1 jquerylib_0.1.4 bslib_0.4.0 vctrs_0.6.5
28## [17] rmarkdown_2.14 tools_4.0.4 stringr_1.5.0 glue_1.6.2
29## [21] xfun_0.31 yaml_2.3.5 fastmap_1.1.0 compiler_4.0.4
30## [25] htmltools_0.5.3 sass_0.4.2
-
Sobald die Größe der Daten von Menschen nicht mehr verarbeitet werden kann, kommen Statistik und Computer zum Einsatz. Sobald die Größe der Daten von üblichen Computern kaum noch verarbeitet werden kann spricht man von “Big Data”. ↩︎
-
Ich klammere den Modus in diesem Tutorial weitgehend aus, um den Fokus auf die in der Praxis wichtigeren Lageparameter zu legen. ↩︎
-
Gewürfelt ist hier wörtlich gemeint, die Daten sind zufällig aus einer Verteilung generiert. ↩︎
-
Der Flynn-Effekt verschiebt die Verteilung regelmäßig, weshalb Tests immer wieder angepasst werden müssen. Ich vermute aber, der Flynn-Effekt ist vor allem ein Problem der Position des Mittelwerts der Verteilung und nicht der Form der Verteilung an sich. ↩︎